【数据结构导论】第三章-栈、队列和数组

发表于 更新于 分类于 本文字数： 2.3k 阅读时长 ≈ 8 分钟

笔记目录

栈及其顺序实现和链接实现

栈的概念

栈（Stack）是运算受限的线性表，这种线性表的插入和删除运算限定在表的某一端进行。允许进行插入和删除的一端为栈顶，另一端为栈底。不含任何数据元素的栈称为空栈。处于栈顶位置的数据元素称为栈顶元素。

栈的后进先出特征

栈的修改原则是后进先出（Last In First Out），因此栈又称为后进先出线性表，简称后进先出表。栈的插入和删除运算分别称为进栈和出栈。

栈的基本运算

  1. 初始化 InitStack(S) 构造一个空栈
  2. 判栈空 Empty(S) 若为空栈返回 1，否则返回 0
  3. 进栈 Push(S,x) 将元素 x 插入栈 S 中，使 x 成为 S 的栈顶
  4. 出栈 Pop(S,) 删除栈顶元素
  5. 取栈顶 GetTop(S) 返回栈顶元素

栈顶和栈底

允许进行插入和删除的一端为栈顶，另一端为栈底

顺序栈的组织方法及其类 C 语言描述

栈的顺序存储结构是用一组连续的存储单元依次存放栈中的每个元素，并用始端作为栈底。

栈的顺序实现成为顺序栈。

通常用一个一维数组和一个记录栈顶位置的变量来实现栈的顺序存储。

类 C 语言描述：

1
2
3
4
5
6
7
const int maxsize = 6; //顺序栈的容量
typedef static seqstack
{
    DataType data[maxsize]; //存储顺序栈中数据元素的数组
    int top;                //标志栈顶位置的变量
}
SeqStack;

顺序栈栈满和栈空的条件

  • 判断栈满：标志栈顶位置的变量等于顺序栈的容量-1

if(stk->top == maxsize - 1)

  • 判断栈空:标志栈顶位置的变量等于 0

if(stk->top == 0)

链栈的组织方法及其类 C 语言描述

栈的链接实现称为链栈，链栈可以用带头结点的单链表来实现。

类 C 语言描述：

typedef struct node
{
    DataType data;
    struct node *next;
} LKStk;

链栈为空的条件

头结点next域为NULL

LS->next == NULL

采用顺序存储和链存储实现栈的基本运算的算法

栈的基本运算在顺序栈上的实现算法

  • 初始化
int InitStack(SeqStack *stk)
{
    stk->top = 0;
    return 1;
}
  • 判栈空
1
2
3
4
5
6
7
8
int EmptyStack(SeqStack *stk)
{
    //若栈为空，返回1，否则返回0
    if (stk->top == 0)
        return 1;
    else
        return 0;
}
  • 进栈
1
2
3
4
5
6
7
8
9
10
11
12
int Push(SeqStack *stk, DataType x)
{
    //若栈未满，元素x进栈stk中，否则报错
    if (stk->top == maxsize - 1)
    { //判断栈是否已满
        error("栈已满");
        return 0;
    }
    stk->top++;              //top值加1
    stk->data[stk->top] = x; //x入栈
    return 1;
}
  • 出栈
1
2
3
4
5
6
7
8
9
10
11
int Pop(SeqStack *stk)
{
    //出栈首先判断是否是空栈
    if (EmptyStack(stk))
    {
        error("下溢");
        return 0;
    }
    stk->top--; //栈顶元素出栈,top-1
    return 1;
}
  • 取栈顶元素
1
2
3
4
5
6
7
8

DataType GetTop(SeqStack *stk)
{
    //取栈顶数据元素，通过返回值返回
    if (EmptyStack(stk))
        return NULLData;
    return stk->data[stk->top];
}

栈的基本运算在链栈上的实现算法

  • 初始化
void initStack(LKStk *LS)
{ //建立一个空栈
    LS = (LS *)malloc(sizeof(LKStk));
    LS->next = NULL;
}
  • 判栈空
1
2
3
4
5
6
7
8
int EmptyStack(LKStk *LS)
{
    //若栈为空返回1，否则返回0
    if (LS->next == NULL)
        return 1;
    else
        return 0;
}
  • 进栈
1
2
3
4
5
6
7
8
void Push(LKStk *LS, DataType x)
{
    LKStk *temp;
    temp = (LK *)malloc(sizeof(LKStk)); //temp指向新申请的结点
    temp->data = x;                     //temp的data域赋值为x
    temp->next = LS->next;              //temp的next域赋值为原来的栈顶结点
    LS->next = temp;                    //指向新的栈顶结点
}
  • 出栈
1
2
3
4
5
6
7
8
9
10
11
12
13
int Pop(LKStk *LS)
{
    //栈顶元素通过参数返回，它的直接后继成为新的栈顶
    LKStk *temp;
    if (!(EmptyStack(LS)))
    {                          //栈不为空
        temp = LS->next;       //temp指向栈顶结点
        LS->next = temp->next; //原栈顶下一个结点成为新的栈顶
        free(temp);            //释放原栈顶结点空间
        return 1;
    }
    return 0;
}
  • 取栈顶元素
1
2
3
4
5
6
7
8
9
DataType GetTop(LKStk *LS)
{
    //取栈顶元素,通过返回值返回
    if (!EmptyStack(LS))
    { //如果不为空栈
        return LS->next->data;
    }
    return NULLData; //否则返回NULLData
}

队列及其顺序实现和链接实现

队列的概念

队列(Queue)是有限个同类型数据元素的线性序列，是一种先进先出(FirstIn First Out)的线性表。

队列的先进先出基本特征

新加入的队列元素加在队列尾端，出队列的数据元素在队列首部被删除。

队列的基本运算

  1. 队列初始化 InitQueue(Q) : 设置一个空队列 Q；
  2. 判队列空 Empty(Q) : 若队列 Q 为空，返回 1，否则返回 0
  3. 入队列 EnQueue(Q,x) : 将数据元素 x 从队列尾端插入队列
  4. 出队列 OutQueue(Q) : 删除队列首元素
  5. 取队列首元素 GetHead(Q) : 返回队列首元素的值

循环队列

队列头尾相接的顺序存储结构叫做循环队列。

队列头和队列尾

顺序存储结构类型中有三个域：data、front、rear。

data 为一维数组

front 为指向队列首元素的前一个单元的指针

rear 为指向队列尾元素单元的指针

顺序队列的组织方法及其类 C 语言描述

一个用于存储队列元素的一维数组和两个分别指示队列首和队列尾的变量，个变量分别称为队列首指针和队列尾指针。

链队列

1
2
3
4
5
6
7
const int maxsize = 20;
typedef struct seqqueue
{
    DataType data[maxsize];
    int front, rear;
} seqQue;
seqQue SQ;

顺序队列满和队列空的条件

队列空：SQ.rear为0，SQ.front为0

队列满:SQ.rear为maxsize

循环队列的组织方法

将存储队列元素的一维数组首尾相接，形成一个环状

循环队列的队列满和队列空的条件

队列满：((CQ.rear + 1) % maxsize == CQ.front)成立
队列空：(CQ.rear == CQ.front)成立

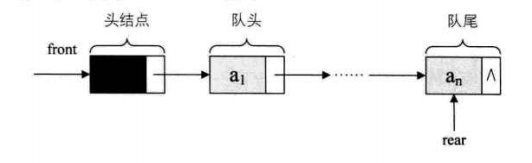
链队列的组织方法及其类 C 语言的描述

使用一个带有头结点的单链表来表示队列，称为链队列。头指针指向单链表头结点，单链表的头结点的 next 域指向队列首结点，尾指针指向队列尾点，即单链表的最后一个结点。

1
2
3
4
5
6
7
8
9
10
typedef struct LinkQueueNode
{
    DataType data;
    struct LinkQueueNode *next;
} LkQueNode;
typedef struct LinkQueueNode
{
    LkQueNode *front, *rear;
} LkQue;
LkQue LQ;

链队列为空的条件

LQ.rear == LQ.front 成立

用数组实现循环队列的基本运算

  • 队列初始化
void InitQueue(CycQue CQ)
{
    CQ.front = 0;
    CQ.rear = 0;
}
  • 判队列空
1
2
3
4
5
6
7
int EmptyQueue(CycQue CQ)
{
    if (CQ.rear == CQ.front)
        return 1;
    else
        return 0;
}
  • 入队列
1
2
3
4
5
6
7
8
9
10
11
int EnQueue(CycQue CQ, DataType x)
{
    if ((CQ.rear + 1) % maxsize == CQ.front)
    { //队列满，入队失败
        error("队列满");
        return 0;
    }
    CQ.rear = (CQ.rear + 1) % maxsize;
    CQ.data[CQ.rear] = x;
    return 1; ///入队列成功
}
  • 出队列
1
2
3
4
5
6
7
8
9
10
int OutQueue(CycQue CQ)
{
    if (EmptyQueue(CQ))
    {
        error("队列空");
        return 0;
    }
    CQ.front = (CQ.front + 1) % maxsize; //出队列
    return 1;
}
  • 取队列首元素
1
2
3
4
5
6
DataType GetHead(CycQue CQ)
{
    if (EmptyQueue(CQ))
        return NULLData; //空队列，返回NULLData
    return CQ.data[(CQ.front + 1) % maxsize];
}

用链表实现队列的基本运算

  • 队列初始化
1
2
3
4
5
6
7
8
void InitQueue(LkQueue *LQ)
{
    LkQueue *temp;
    temp = (LkQueueNode *)malloc(sizeof(LkQueueNode)); //生成队头结点
    LQ->front = temp;                                  //队列头指针指向头结点
    LQ->rear = temp;                                   //队列尾指针指向尾结点
    (LQ->front)->next = NULL;
}
  • 判队列空
1
2
3
4
5
6
int EmptyQueue(LkQueue *LQ)
{
    if (LQ->rear == LQ->front)
        return 1;
    return 0;
}
  • 入队列
1
2
3
4
5
6
7
8
9
void EnQueue(LkQueue *LQ, DataType x)
{
    LkQueueNode *temp;
    temp = (LkQueueNode *)malloc(sizeof(LkQueueNode));
    temp->data = x;
    temp->next = NULL;
    (LQ->rear)->next = temp; //新结点入队列
    LQ->rear = temp;         //新结点为队列尾
}
  • 出队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int OutQueue(LkQueue *LQ)
{
    LkQueueNode *temp;
    if (EmptyQueue(LQ))
    {
        error("队列空");
        return 0;
    }
    temp = (LQ->front)->next;       //temp指向队列首结点
    (LQ->front)->next = temp->next; //使得头结点指针域指向新的首结点
    if (temp->next == NULL)
        LQ->rear = LQ->front; //无首结点，fron和rear都指向头结点
    free(temp);
    return 1;
}
  • 取队列首元素
1
2
3
4
5
6
7
8
DataType GetHead(LkQueue *LQ)
{
    LkQueueNode *temp;
    if (EmptyQueue(LQ))
        return NULLData; //队列空，返回空数据标志
    temp = LQ.front->next;
    return temp->data; //非空，返回队列首结点元素
}

数组及其实现

一维、二维数组的逻辑结构及其顺序存储方法

数组可以看成线性表的一种推广。一维数组又称向量，它由一组具有相同类型的数据元素组成，并存储在一组连续的存储单元中。

二维数组看成 n 个列向量组成的线性表，它可以表示成

a’ =(α0，α1，…，αn-1)

二维数组看成 m 个行向量组成的线性表，它可以表示成

a’’ = (β0，β1，…，βm-1)

顺序存储的一维数组、二维数组的地址计算

loc 为某个求坐标的函数,k 为每个元素所占存储单元

一维数组：loc[i] = loc[0] + i * k

二维数组：loc[i,j] = loc[0,0] + (n * i + j) * k

特殊矩阵（三角矩阵、对称矩阵）的概念

  • 对称矩阵：

    若一个 n 阶方阵 A 中的元素满足下述条件：

    aij = aji;

    0< = i;

    j <= n - 1;

    则 A 称为对称矩阵

  • 三角矩阵：

    以主对角线为界的上/下半部分是一个固定的值 c 或零，这样的矩阵叫做上/下三角矩阵。